4. 编程实现 LeNet 的训练和 U-Net 的补全及测试
姓名:许展风 学号:3210100658
电子邮箱:zhanfeng_xu@outlook.com 联系电话:15224131655
老师:潘纲老师 报告日期:2023年12月29日
4.1. 一、功能简述及运行说明
4.1.1. 1.1 功能简述
实现LeNet-5 的训练,应用于 MNIST 数据集上的手写数字识别任务(图像分类)
实现U-Net 的网络补全与测试,应用于 Carvana 数据集上的掩码 (Mask) 预测任务(语义分割)
4.1.2. 1.2 运行说明
运行lenet.py文件,程序实现LeNet-5的构建,并在MNIST数据集上进行训练和测试,命令行同步输出训练和测试过程,运行完成后保存训练过程的loss曲线与识别率曲线,以及测试过程的识别率曲线图。
运行try.py文件,程序实现U-Net的构建,并加载默认路径下的模型model.pth,输入默认路径下的图片,进行单图片测试,输出图片的预测掩码图。
4.2. 二、开发与运行环境
编程语言:python 3.10.6 torch 2.0.1+cu118 torchvision 0.15.2+cu118
运行环境:Windows
4.3. 三、算法原理
4.3.1. 3.1 CNN网络模型
卷积神经网络(Convolutional Neural Network,CNN)是一种包含卷积运算且具有深度结构的前馈神经网络(Feedforward Neural Network,FNN),被广泛应用于图像识别、自然语言处理和语音识别等领域。一般包含5种类型的网络层次结构:
输入层:卷积网络的原始输入,可以是原始或预处理后的像素矩阵。
卷积层:参数共享、局部连接,利用平移不变性从全局特征图提取局部特征。
激活层:将卷积层的输出结果进行非线性映射。
池化层:进一步筛选特征,可以有效减少后续网络层次所需的参数量。
全连接层:将多维特征展平为二维特征,通常低维度特征对应任务的学习目标(类别或回归值)。
4.3.1.1. 卷积层
卷积层中需要用到卷积核(滤波器或特征检测器)与图像特征矩阵进行点乘运算,利用卷积核与对应的特征感受野进行滑窗式运算时,需要设定卷积核对应的大小、步长、个数以及填充的方式。
卷积核大小(Kernel Size):定义了卷积的感受域。在过去常设为5,如LeNet-5;现在多设为3,通过堆叠3*3的卷积核来达到更大的感受域。
卷积核步长(Stride):定义了卷积核在卷积过程中的步长。常见设置为1,表示滑窗距离为1,可以覆盖所有相邻位置特征的组合;当设置为更大值时相当于对特征组合降采样。
填充方式(Padding):在卷积核尺寸不能完美匹配输入的图像矩阵时需要进行一定的填充策略。通常为零填充或者舍去。
4.3.1.2. 池化层
对于池化层,最大池化(Max Pooling)和平均池化(Average Pooling)是常用的池化操作,用于减少特征图的尺寸,并提取最显著的特征。
最大池化:在每个池化窗口中选择最大值作为输出,可以保留图像区域最显著的特征,对于边缘检测和纹理分析等任务可能更有效。
平均池化:它选择窗口内所有值的平均值,因此更多地考虑整个区域的信息,对图像的全局特征进行了平均处理,对于一些要求更多上下文信息的任务,如目标识别更加有用。
4.3.1.3. LeNet-5
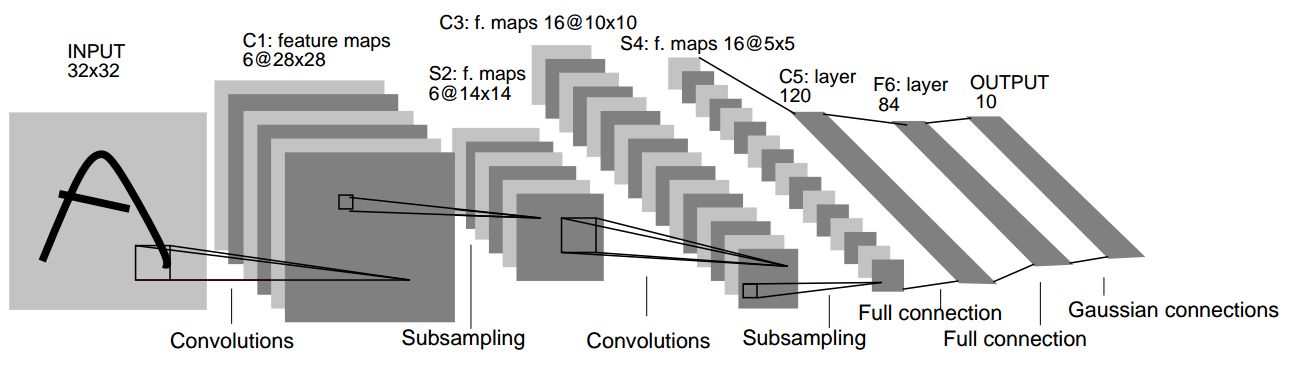
LeNet-5 是由 Yann LeCun 在 1998 年提出的一个经典卷积神经网络(CNN)架构,它是用于手写数字识别任务的早期深度学习模型之一。其架构包含了卷积层、池化层和全连接层。
4.3.1.4. U-Net
U-Net 是一个经典的语义分割全卷积网络,最初应用于医疗图像的分割任务。其网络结构如下图所示,可以看到 U-Net 有一个对称的结构,左边是一个典型的卷积神经网络,右边是一个对称的上采样网络,可以将左边的特征图恢复到原图大小。
左侧向下的结构被称为 Contracting Path,由通道数不断增加的卷积层和池化层组成
右侧向上的结构被称为 Expanding Path,由通道数不断减少的卷积层和上采样层(反卷积层)组成
在 Expanding Path 中,每次上采样层都会将 Contracting Path 中对应的特征图与自身的特征图进行拼接,这样可以保证 Expanding Path 中的每一层都能够利用 Contracting Path 中的信息
4.3.1.5. 数据集
MNIST 数据集是一个常用的机器学习基准数据集,由 0 到 9 的手写数字图像组成,每个图像都是 28x28 像素的灰度图像。torchvision.datasets.MNIST 模块提供了一种简单的方式来下载、加载和预处理 MNIST 数据集,使其能够被用于训练和测试深度学习模型。这个模块一般与 PyTorch 的 DataLoader 结合使用,以便对数据进行批处理、洗牌等操作,并将数据提供给神经网络模型进行训练或评估。
Carvana 数据集是 kaggle 上的一个语义分割竞赛数据集,目标是实现对汽车的分割。根据 Carvana 数据集的划分,其训练集包含 5088 张汽车图片 (.jpg) 和对应的掩码 (mask, .gif),掩码可以认为是 0-1 的,表示图片上每个像素是否属于汽车。因此这个问题可以处理成逐像素的二分类问题。
4.3.2. 3.2 网络训练与测试
4.3.2.1. 正向传播(forward)
正向传播是指对神经网络沿着从输入层到输出层的顺序,依次计算并存储模型的中间变量(包括输出)。
4.3.2.2. 反向传播(Backpropagation,BP)
反向传播(Backpropagation,BP)是“误差反向传播”的简称,是一种与最优化方法(如梯度下降法)结合使用的,用来训练人工神经网络的常见方法。该方法对网络中所有权重计算损失函数的梯度。这个梯度会反馈给最优化方法,用来更新权值以最小化损失函数。
4.3.2.3. 优化器(Optimizer)
optimizer 对象够保持当前参数状态并基于计算得到的梯度进行参数更新。在 PyTorch 中,可以使用 torch.optim 模块来创建优化器对象,用于更新神经网络模型的参数,以最小化定义的损失函数。torch.optim 包含了许多常用的优化算法,比如 SGD、Adam、RMSprop 等。
随机梯度下降优化器(SGD):基本的优化算法之一。它通过计算当前样本的梯度来更新模型的参数,每次迭代仅考虑一个样本的梯度。SGD的核心思想是沿着梯度的反方向更新参数,以减小损失函数。然而,SGD可能会收敛速度较慢,并且可能在参数空间中摆动。
参数:
learning_rate(学习率):控制每次参数更新的步长大小。默认值为0.01。学习率的选择对模型的收敛和性能至关重要。如果学习率过大,可能会导致震荡或无法收敛;如果学习率过小,收敛速度可能很慢。momentum(动量):用于加速SGD在相关方向上的移动,避免陷入局部极小值。通常设置在0.9左右。dampening(阻尼项):动量的阻尼系数,用于减少动量的影响。通常默认为0。
自适应矩估计(Adam):是一种结合了动量和自适应学习率调整的优化算法,通过计算梯度的一阶矩估计和二阶矩估计来动态调整学习率。Adam能够根据梯度的大小自适应地调整每个参数的学习率,因此对于不同参数的学习率可以有不同的变化。
参数:
learning_rate(学习率):控制参数更新的步长大小。默认值为0.001。betas(动量项的衰减因子):通常设置为(0.9, 0.999),用于计算梯度的一阶矩估计(均值)和二阶矩估计(方差)。eps(数值稳定性):用于避免除以零的情况。默认值为1e-8。weight_decay(权重衰减):L2正则化的参数,用于对模型参数进行惩罚,防止过拟合。默认值为0。
4.3.2.4. 损失函数(Loss Function)
用于衡量模型预测值与实际值之间的差异,它是机器学习模型优化过程中的核心部分。损失函数的选择影响着模型的训练效果和最终的性能。其目标是尽量减小预测值与实际值之间的差异,从而使模型能够更好地拟合训练数据并提高泛化能力。在 PyTorch 中,定义损失函数主要通过 torch.nn 模块下的各种损失函数类来完成。
均方误差(Mean Squared Error, MSE):它计算预测值与真实值之间差的平方的均值。
交叉熵损失(Cross Entropy Loss):常用于分类任务中,特别是多类别分类问题。对于二分类问题,使用二元交叉熵,对于多分类问题,使用多元交叉熵。
KL散度(Kullback-Lerbler Divergence):KL散度用于度量两个概率分布之间的差异,通常在模型训练过程中作为正则化项使用。
4.4. 四、具体实现
4.4.1. 4.1 LeNet-5 的训练
4.4.1.1. 构建网络
# 定义 LeNet-5 神经网络结构模型
class Model(nn.Module):
def __init__(self):
super(Model, self).__init__() # 利用参数初始化父类
self.conv1 = nn.Conv2d(1, 6, kernel_size=5)
self.avgpool1 = nn.AvgPool2d(kernel_size=2, stride=2)
self.conv2 = nn.Conv2d(6, 16, kernel_size=5)
self.avgpool2 = nn.AvgPool2d(kernel_size=2, stride=2)
self.fullconnection1 = nn.Linear(16 * 4 * 4, 120)
self.fullconnection2 = nn.Linear(120, 84)
self.fullconnection3 = nn.Linear(84, 10)
# 定义前向传播
def forward(self, x):
x = self.avgpool1(F.relu(self.conv1(x)))
x = self.avgpool2(F.relu(self.conv2(x)))
x = x.view(-1, 16 * 4 * 4)
x = F.relu(self.fullconnection1(x))
x = F.relu(self.fullconnection2(x))
x = self.fullconnection3(x)
return x
在构建网络结构时,需要特别注意的是每层结构的具体参数,在关注计算核、步长的选取时,还要注意输入输出的维度,需要前后对应。x = x.view(-1, 16 * 4 * 4)用于将张量展平。
4.4.1.2. 载入数据
# 定义数据预处理
transform = transforms.ToTensor()
# 下载数据到指定位置
trainset = datasets.MNIST(root,
train=True,
transform=transform,
target_transform=None,
download=True)
testset = datasets.MNIST(root,
train=False,
transform=transform,
target_transform=None,
download=True)
# 提取数据
train_loader = torch.utils.data.DataLoader(trainset,
batch_size=64,
shuffle=True)
test_loader = torch.utils.data.DataLoader(testset,
batch_size=64,
shuffle=False)
数据预处理可以包括转张量、归一化等操作,提取数据时,几个参数需要注意:
batch_size指在深度学习中用于训练的每个小批量(mini-batch)样本的数量。合适的大小可以缓解内存压力、提高训练速度与模型泛化能力。
shuffle,用于指示在每个 epoch 开始时是否对数据进行随机打乱。它控制着在每个 epoch 开始时是否对数据进行重新排序,以避免模型每次都在相同的顺序下进行训练。
4.4.1.3. 其他函数构建
# 实例化模型
model = Model().to(device)
# 实例化损失函数
criterion = nn.CrossEntropyLoss() # 交叉熵损失,用于多分类问题
# 构建优化器
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
在这里,可以定义损失函数、优化器模型,可以设置模型的学习率lr。
4.4.1.4. 模型训练与测试
for epoch in range(num_epochs):
for batch_index, (data, targets) in enumerate(train_loader):
# 数据装载
data = data.to(device)
targets = targets.to(device)
# 训练
optimizer.zero_grad() # 梯度清零
y_pred = model(data) # 正向传播
loss = criterion(y_pred, targets) # 计算损失
loss.backward() # 反向传播计算损失函数梯度
optimizer.step() # 更新参数
# 记录当前的识别率
_, prediction = torch.max(y_pred, 1)
train_percents.append(
torch.sum(prediction == targets).item() / len(targets))
# 每次训练结束,保存最终识别率
train_accuracy.append(sum(train_percents) / len(train_percents))
# 每次训练后进行测试
test_percents = [] # 用于记录每batch测试的识别率
with torch.no_grad():
for data, targets in test_loader:
# 数据装载
data = data.to(device)
targets = targets.to(device)
# 正向传播
test_y_pred = model(data)
# 记录识别率
_, test_prediction = torch.max(test_y_pred, 1)
test_percents.append(
torch.sum(test_prediction == targets).item() / len(targets))
# 每次测试结束,保存最终的识别率
test_accuracy.append(sum(test_percents) / len(test_percents))
训练与测试的核心代码如上,两个循环,循环epoch,指训练次数,由于训练集的提取是shuffer随机打乱后的,多次训练能够不断优化网络参数;循环batch,是按批次训练或测试数据,此时我们选择每batch梯度清零,就要在batch循环内更新参数,如果选择每batch梯度叠加,则相当于将小批次合成大批次,需要合理调整模型更新、梯度清零的时机。
识别率的提取通过_, test_prediction = torch.max(test_y_pred, 1)在第二个维度上提取最大值的序号,作为输出类别标签,与数据集中的标签对比得到识别率。
4.4.2. 4.2 U-Net补全与测试
class CropAndConcat(nn.Module):
def forward(self, x: torch.Tensor, contracting_x: torch.Tensor):
"""
:param x: current feature map in the expansive path
:param contracting_x: corresponding feature map from the contracting path
"""
b, c, h, w = x.shape
# TODO: Concatenate the feature maps
# use torchvision.transforms.functional.center_crop(...)
x = torch.cat((x, center_crop(contracting_x, (h, w))), dim=1)
return x
U-Net网络最关键的拼接函数,根据网络结构描述可知,拼接时是按通道数(channel)这一维度拼接,对应张量的dim=1的维度,同时contracting path的张量需要从中心裁切为和x相同的大小,对应(h,w)的维度。同时注意拼接的位置,x在左。
剩余的结构不全只需关注参数设置,以及forward传递时,保留待拼接的张量。按网络结构顺序编写即可。
4.4.2.1. 测试预处理
# 定义预处理
transform = transforms.Compose(
[transforms.Resize([572, 572]),
transforms.ToTensor()])
# 调整大小为572×572,转为张量,增加维度B
input_x_tensor = transform(input_x).unsqueeze(0)
Image.open读入图片后,预处理,将图片大小插值调整为572×572,同时通过unsqueeze(0)增加张量的维度,增加后张量维度为(1,3,572,572)。通过 model = UNet(in_channels=3, out_channels=1).to(device)这一给定的模型参数定义程序,得知模型输入通道数为3,因此可将处理后的张量输入模型了。
# score.shape = (1, 1, w, h)
# 输出结果插值处理,匹配图片尺寸
img_size = (img.size[1], img.size[0])
score = F.interpolate(score,
size=img_size,
mode="nearest")
score = score.squeeze() # 移除尺度为1的维度, score.shape = (w, h)
score = F.sigmoid(score) # sigmoid函数处理
threshold = 0.8 # 设定阈值,不能超过1,过小效果变差
mask = (score > threshold) # 根据阈值转换
mask = mask.cpu().numpy().astype(int) # 张量迁移至cpu,转为整数数组
plot_img_and_mask(img, mask) # 输出结果图片
使用interpolate通过插值处理变换张量的维度,变为输入图片的大小,再通过squeeze,移去多余的维度。经过合适的阈值判断处理后得到张量mask,它的类型是bool。绘制mask还需要转为整数数组,此时需要将张量转移到CPU后再转为整数数组。调整阈值可以得到不同的输出结果。
4.5. 五、实验结果与分析
4.5.1. 5.1 LeNet-5
在选择损失函数为交叉熵损失,优化器类型为自适应矩估计,学习率为0.001,batch_size为64,训练次数为10的情况下,得到结果如下:

可以看到随着训练次数的增加,loss值,即模型预测值与实际值之间的差异越来越小,逼近于0。说明模型在一步步优化。同时第二次训练后的结果最为明显,随着次数增加,训练对loss的减小效果越来越弱。

同时训练集的识别率与上图是对应的,随着训练次数增加,识别率显著提升,但提升效果越来越弱。

测试集的识别率曲线展现了相似的趋势,事实上即使是epoch=0,模型也能给出非常高的识别率,这主要原因在于其实在一个epoch中有都多个batch循环,已经对模型进行了数次训练,一个epoch是对所有数据集遍历后的结果,而不止是一次前向传播、反向传播、模型更新的结果。最终测试集的识别率达到98.9%。
4.5.2. 5.2 U-Net补全与测试
模型成功装载后,测试图片,选择阈值为0.8,得出结果如下:

可以看到模型成功分割出图片中的汽车,即判断出图片中的元素是否属于汽车,解出这个二分类问题。
当选择的阈值为0.5左右或高于0.8小于1时,模型也能完成分割任务,但输出结果中会有一定边缘毛刺,当阈值过低,模型将不能完成任务,输出的掩码中将大部分像素判断为1。
4.6. 六、结论与心得体会
4.6.1. 结论
该程序能够基本完成LeNet-5重构,训练,识别的任务,对测试集的识别率能够达到98%以上。
同时补全后的程序能够基本完成U-Net单图片测试任务,输出正确的结果图片。
4.6.2. 心得体会
LeNet-5程序编写的过程中,代码逻辑比较简单,但是需要了解很多对各个函数的使用、参数确定的涵义等相关知识。有些参数的确定建立在模型、数据的特性上,有些参数则主要根据前人的经验判断。
例如损失函数的选择,根据解决问题的性质是多分类问题,因此选择交叉熵损失。
例如batch_size的选择,更好的方法是从小到大依次实验,选择合适的参数,因为它也跟硬件条件有关,在本实验中为了节省不必要的时间成本,选择了常用的64。
另外优化器的选择意料之外的重要,当选择随机梯度优化(SGD)时,由于其下降速度慢,导致模型训练效果不明显。
当对LeNet-5的网络结构编写有一定了解后,U-net的结构也能够更好的理解和掌握。而且已经给出了大致代码框架的前提下,省去了很多时间,可以直接去思考如何编写核心的代码。理解结构、编写代码不难,难得是不清楚为何要有这样的结构,为何确定这样的维数输入输出。
U-Net实验中一开始没有明白实例化的模型
model = UNet(in_channels=3, out_channels=1).to(device)和文件中给出的model.pth有什么关系,后来理解为model.pth是U-Net网络模型训练后得到的模型参数,因此加载后可以直接测试图片。在无论是LeNet-5还是U-Net测试的过程中,都遇到过一个困惑,就是不清楚这个网络输出结果的具体意义是什么,只是单纯可以确定它的维数。如果已知训练过程,可以从损失函数与targets来推断,但是未知训练过程下,这个模型输出就觉得会有些抽象化。当然U-Net的文档说明给出了对输出结果处理的描述,因此可以较为顺利地得出mask。
之前的数据类型建立在Numpy上,是向量,而PyTorch的数据类型是张量,它们有些相同点,也有更多的不同点,编写时需要格外注意变量的数据类型。
4.7. 七、参考文献
[1],罗小罗同学,卷积神经网络(CNN), [OL],知乎, 2023-5-7, [2023-12-30],卷积神经网络(CNN) - 知乎 (zhihu.com)